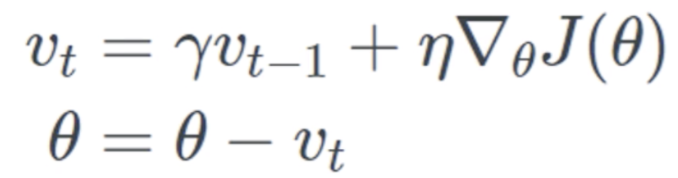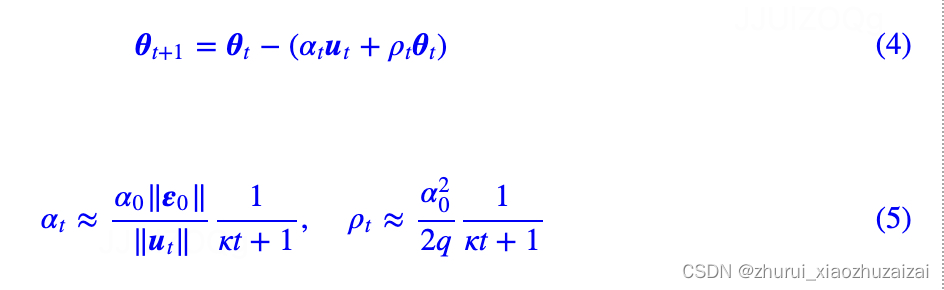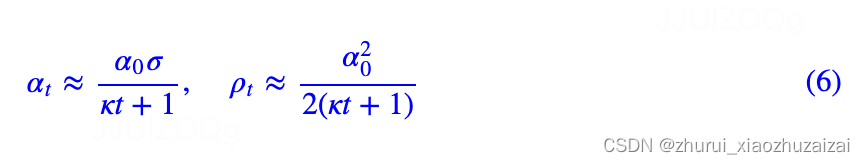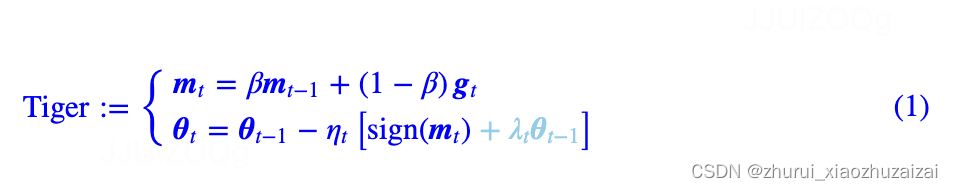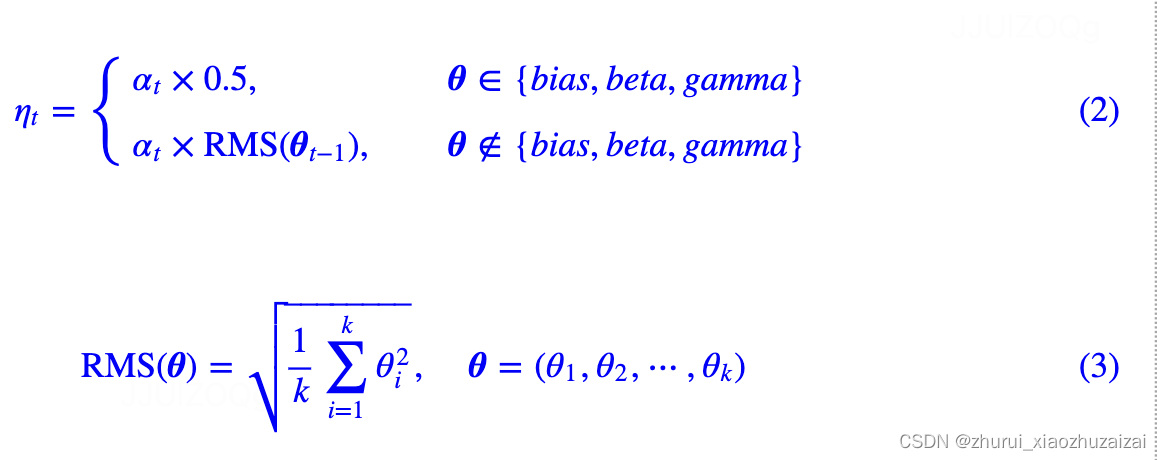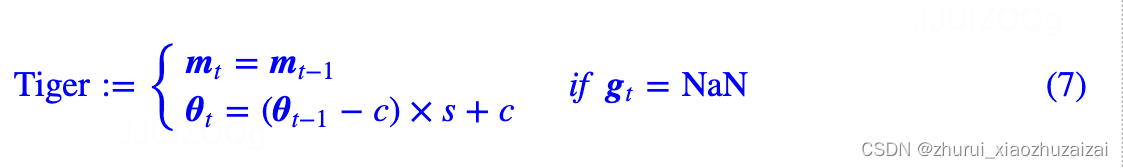常用的优化方法和优化函数[梯度下降SGD,牛顿法,ada系列(adagrad, rmsprop,adadelta,adam),lion, tiger]+炼丹策略
逻辑回归本身是可以用公式求解的,但是因为需要求逆的复杂度太高,所以才引入了梯度下降算法。
一阶方法:梯度下降、随机梯度下降、mini
随机梯度下降降法。随机梯度下降不但速度上比原始梯度下降要快,局部最优化问题时可以一定程度上抑制局部最优解的发生。
二阶方法:牛顿法、拟牛顿法:
这里详细说一下牛顿法的基本原理和牛顿法的应用方式。牛顿法其实就是通过切线与x轴的交点不断更新切线的位置,直到达到曲线与x轴的交点得到方程解。在实际应用中我们因为常常要求解凸优化问题,也就是要求解函数一阶导数为0的位置,而牛顿法恰好可以给这种问题提供解决方法。实际应用中牛顿法首先选择一个点作为起始点,并进行一次二阶泰勒展开得到导数为0的点进行一个更新,直到达到要求,这时牛顿法也就成了二阶求解问题,比一阶方法更快。我们常常看到的x通常为一个多维向量,这也就引出了Hessian矩阵的概念(就是x的二阶导数矩阵)。
缺点:牛顿法是定长迭代,没有步长因子,所以不能保证函数值稳定的下降,严重时甚至会失败。还有就是牛顿法要求函数一定是二阶可导的。而且计算Hessian矩阵的逆复杂度很大。
拟牛顿法:
不用二阶偏导而是构造出Hessian矩阵的近似正定对称矩阵的方法称为拟牛顿法。拟牛顿法的思路就是用一个特别的表达形式来模拟Hessian矩阵或者是他的逆使得表达式满足拟牛顿条件。主要有DFP法(逼近Hession的逆)、BFGS(直接逼近Hession矩阵)、
L-BFGS(可以减少BFGS所需的存储空间)。
当目标函数是凸函数时,梯度下降法的解是全局解。一般情况下,其解不保证是全局最优解,梯度下降法的速度也未必是最快的。梯度下降法的优化思想是用当前位置负梯度方向作为搜索方向,因为该方向为当前位置的最快下降方向,所以也被称为是”最速下降法“。
梯度下降法的缺点:
最速下降法越接近目标值,步长越小,前进越慢。
梯度下降法的最大问题就是会陷入局部最优,靠近极小值时收敛速度减慢。
靠近极小值时收敛速度减慢,如下图所示;
直线搜索时可能会产生一些问题;
可能会“之字形”地下降。
批量梯度下降法
最小化所有训练样本的损失函数,使得最终求解的是全局的最优解,即求解的参数是使得风险函数最小,但是对于大规模样本问题效率低下。随机梯度下降法
最小化每条样本的损失函数,虽然不是每次迭代得到的损失函数都向着全局最优方向,但是大的整体的方向是向全局最优解的,最终的结果往往是在全局最优解附近,适用于大规模训练样本情况。
随机梯度下降是通过每个样本来迭代更新一次,如果样本量很大的情况(例如几十万),那么可能只用其中几万条或者几千条的样本,就已经将theta迭代到最优解了,对比上面的批量梯度下降,迭代一次需要用到十几万训练样本,一次迭代不可能最优,如果迭代10次的话就需要遍历训练样本10次。但是,SGD伴随的一个问题是噪音较BGD要多,使得SGD并不是每次迭代都向着整体最优化方向。minibatch
将您的数据集分成几个batches。这样,它就不必等到算法遍历整个数据集后才更新权重和偏差,而是在每个所谓的Mini-batch结束时进行更新。这使得我们能够快速将成本函数移至全局最小值,并在每个epoch中多次更新权重和偏差。最常见的Mini-batch大小是16、32、64、128、256和512
牛顿法是一种在实数域和复数域上近似求解方程的方法。方法使用函数f (x)的泰勒级数的前面几项来寻找方程f (x) = 0的根。牛顿法最大的特点就在于它的收敛速度很快。
牛顿法比梯度下降法快
牛顿法是二阶收敛,梯度下降是一阶收敛,所以牛顿法就更快。如果更通俗地说的话,比如你想找一条最短的路径走到一个盆地的最底部,梯度下降法每次只从你当前所处位置选一个坡度最大的方向走一步,牛顿法在选择方向时,不仅会考虑坡度是否够大,还会考虑你走了一步之后,坡度是否会变得更大。所以,可以说牛顿法比梯度下降法看得更远一点,能更快地走到最底部。
但是牛顿法要算hessian矩阵的逆,比较费时间。
拟牛顿法的本质思想是改善牛顿法每次需要求解复杂的Hessian矩阵的逆矩阵的缺陷,它使用正定矩阵来近似Hessian矩阵的逆,从而简化了运算的复杂度。拟牛顿法和最速下降法一样只要求每一步迭代时知道目标函数的梯度。通过测量梯度的变化,构造一个目标函数的模型使之足以产生超线性收敛性。这类方法大大优于最速下降法,尤其对于困难的问题。另外,因为拟牛顿法不需要二阶导数的信息,所以有时比牛顿法更为有效。常用的拟牛顿法有DFP算法和BFGS算法。
共轭梯度法是介于最速下降法与牛顿法之间的一个方法,它仅需利用一阶导数信息,但克服了最速下降法收敛慢的缺点,又避免了牛顿法需要存储和计算Hesse矩阵并求逆的缺点,共轭梯度法不仅是解决大型线性方程组最有用的方法之一,也是解大型非线性最优化最有效的算法之一。
在各种优化算法中,共轭梯度法是非常重要的一种。其优点是所需存储量小,具有步收敛性,稳定性高,而且不需要任何外来参数。
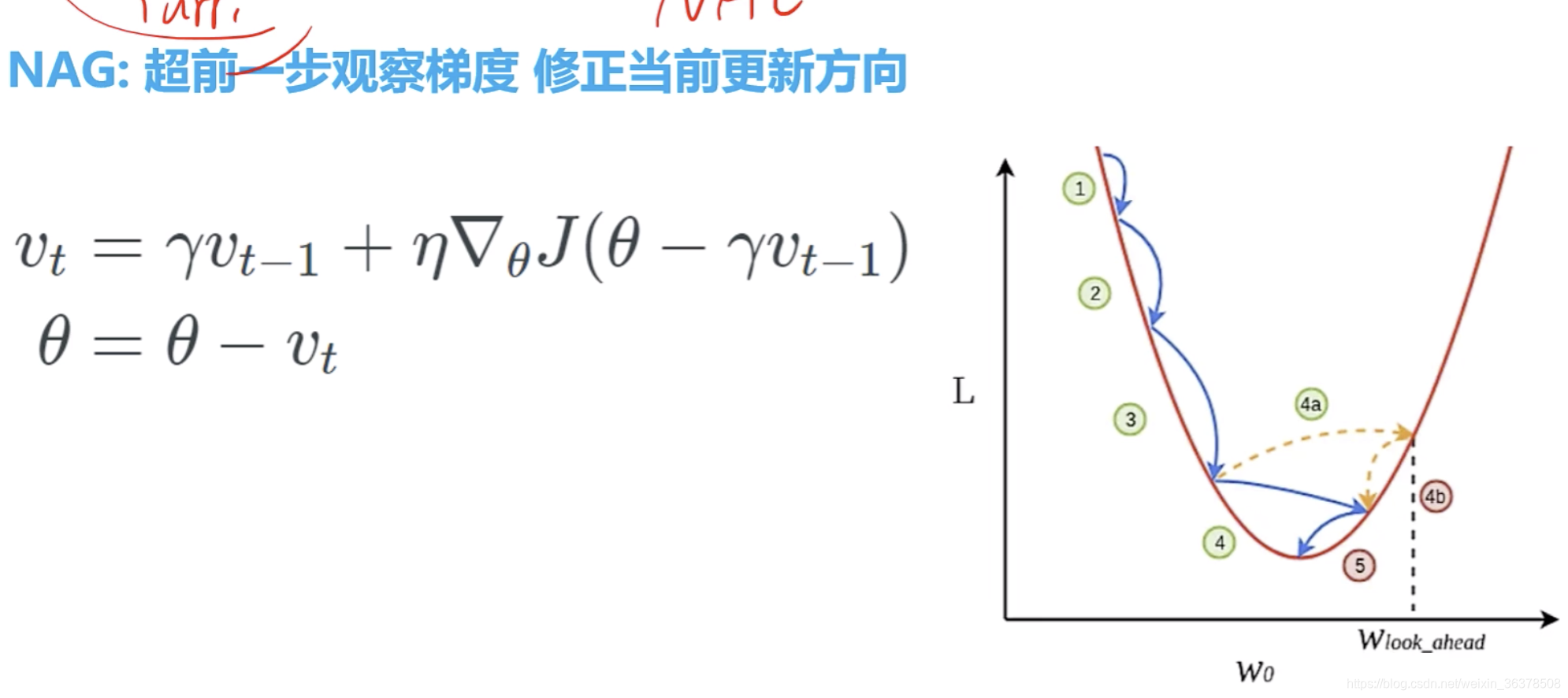
类比惯性
参数更新时,不光考虑当前的梯度方向,还要考虑过去累积梯度的方向,但需要乘以衰减系数(类比摩擦力)
可以减小落在局部最小值的概率,但不能避免
既考虑动量,又考虑二阶导的变化趋势
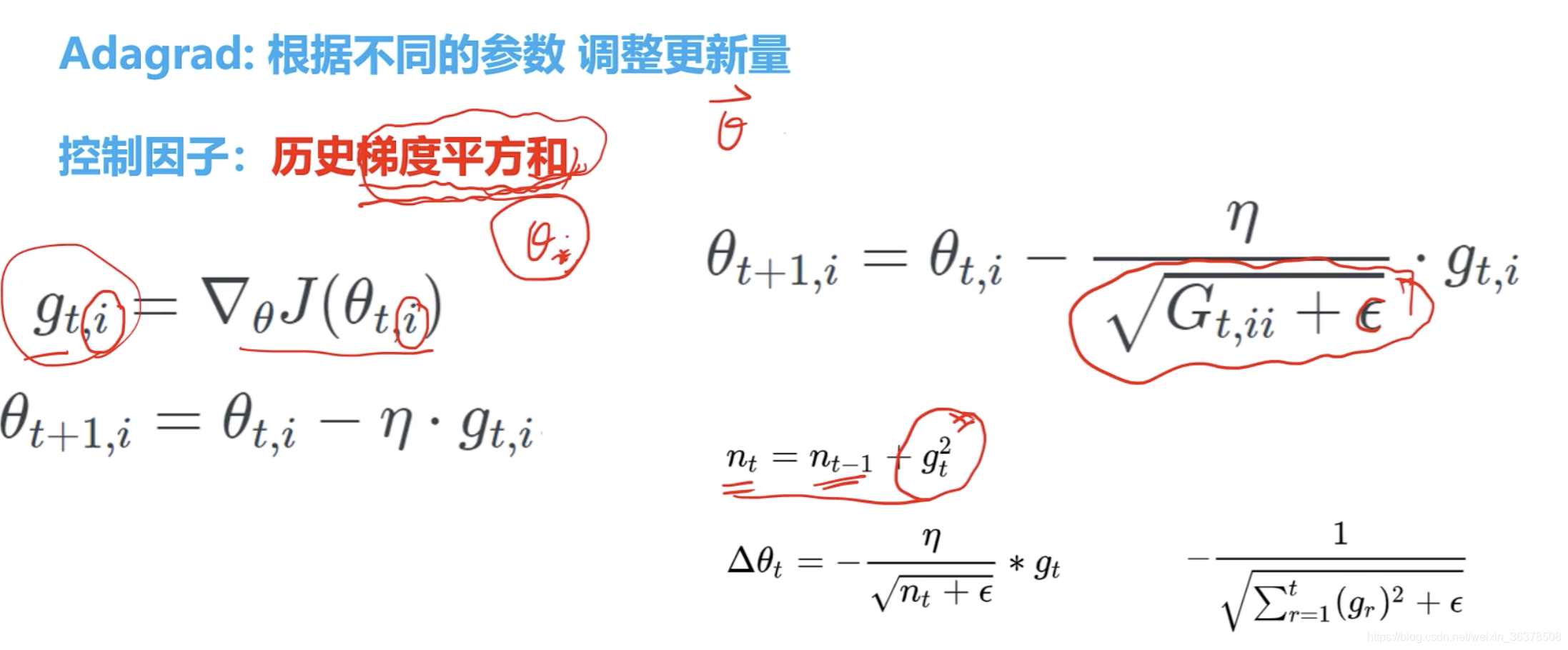
每个参数调整更新量。
对于那些梯度小的参数,将梯度放大
对于那些梯度大的参数,将梯度缩小 控制因子:历史梯度平方和
缺点:随着时间的累加,更新一定越来越慢,因为分母越来越大。
Gt,ii过去梯度的平方和,加上epsilon避免为0
nt为所有时刻梯度的平方和
分母并不会随着时间变得特别大
因为0.9 和0.1等于1,所以不会增大
不需要设置初始学习率了,可以自己计算
mt:用gt的一次更新 ,动量
vt:用gt的平方更新
mt初始:除以1-beta1,最开始时,让梯度迈得大一点算法计算了梯度的指数移动均值(exponential moving average),超参数 beta1 和 beta2 控制了这些移动均值的衰减率。移动均值的初始值和 beta1、beta2 值接近于 1(推荐值),因此矩估计的偏差接近于 0。该偏差通过首先计算带偏差的估计而后计算偏差修正后的估计而得到提升。

SGD里面,梯度真正有用的是方向而不是大小。所以,即使你只保留梯度的符号来对模型进行更新,也能得到收敛的效果。甚至有些情况下,这么做能减少梯度的噪声,使得收敛速度更快。
直接把 gradient 求 sign

把 momentum 求 sign


论文:Symbolic Discovery of Optimization Algorithms
from:Google
主要内容:自动搜索优化器的
方式:通过数千TPU小时的算力搜索并结合人工干预,得到了一个速度更快、显存更省的优化器Lion(EvoLved Sign Momentum),并在图像分类、图文匹配、扩散模型、语言模型预训练和微调等诸多任务上做了充分的实验,多数任务都显示Lion比目前主流的AdamW等优化器有着更好的效果。
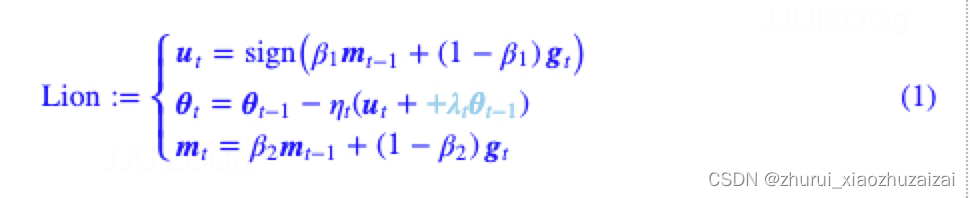
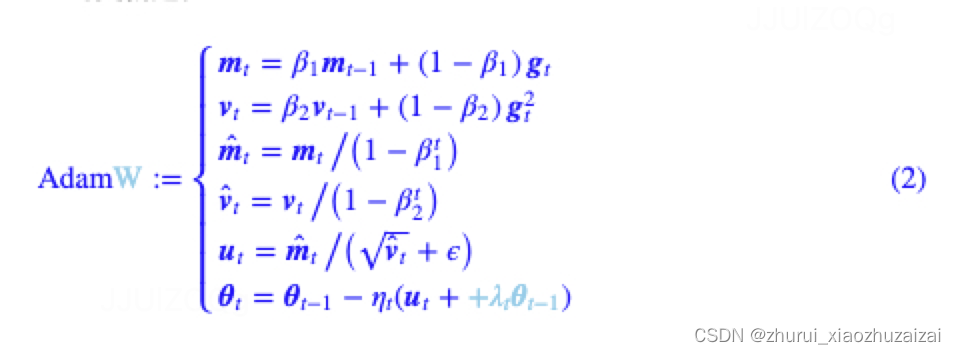
Lion相比AdamW参数更少(少了个?),少缓存了一组参数v(所以更省显存),
并且去掉了AdamW更新过程中计算量最大的除法和开根号运算(所以更快)。
跟Lion一样,SIGNUM也用到了符号函数处理更新量,而且比Lion更加简化(等价于Lion在β1=β2和λt=0的特例),但是很遗憾,SIGNUM并没有取得更好的效果,它的设计初衷只是降低分布式计算中的传输成本。Lion的更新规则有所不同,尤其是动量的更新放在了变量的更新之后,并且在充分的实验中显示出了它在效果上的优势
首先是β1,β2,原论文自动搜索出来的结果是β1=0.9,β=0.99,并在大部分实验中复用了这个组合,
但是在NLP的任务上则使用β1=0.95,β2=0.98这个组合(论文的详细实验配置在最后一页的Table 12)。
比较关键的学习率η和权重衰减率λ,由于Lion的更新量u每个分量的绝对值都是1,这通常比AdamW要大,所以学习率要缩小10倍以上,才能获得大致相同的更新幅度;而由于学习率降低了,那么为了使权重衰减的幅度保持不变,权重衰减率应该要放大相应的倍数。原论文的最后一页给出了各个实验的超参数参考值,其中小模型(Base级别)上使用的是η=3×10?4和λ=0.01,大模型(参数10亿以上)则适当降低了学习率到η=2×10?4甚至η=10?4。
在该方案中,更新量写为
其中ut是原本的更新量;α0是(初始阶段)参数变化的相对大小,一般是10?3级别,表示每步更新后参数模长的变化幅度大致是千分之一;>q是一个超参数,没什么特殊情况可以设为1;κ是控制学习率衰减速度的超参数,可以根据训练数据大小等设置。
由于ut经过了sign运算,因此‖ut‖=√k,k是参数的维度;
‖ε0‖≈k√σ,这我们在《基于Amos优化器思想推导出来的一些“炼丹策略”》已经推导过了,其中σ是参数的变化尺度,对于乘性矩阵,σ2
就是它的初始化方差。所以,经过一系列简化之后,有
这里的αt就是前面的ηt,而λt=ρt/αt=α0/2σ。
按照BERT base的d=768来算,初始化方差的量级大致在1/d左右,于是σ=√(1/d)≈0.036,假设α0取1.11×10?3(为了给结果凑个整),那么按照上式学习率大约是4×10?5、衰减率大约是0.015。在笔者自己的MLM预训练实验中,选取这两个组合效果比较好。
自Adam提出以来,由于其快速收敛的特性成为了很多模型的默认优化器。甚至有学者提出,这个现象将反过来导致一个进化效应:所有的模型改进都在往Adam有利的方向发展,换句话说,由于我们选择了Adam作为优化器,那么就有可能将很多实际有效、但是在Adam优化器上无效的改动都抛弃了,剩下的都是对Adam有利的改进,详细的评价可以参考《NEURAL NETWORKS (MAYBE) EVOLVED TO MAKE ADAM THE BEST OPTIMIZER》。所以,在此大背景之下,能够发现比Adam更简单且更有效的优化器,是一件很了不起的事情,哪怕它是借助大量算力搜索出来的。
可能读者会有疑问:Lion凭啥可以取得更好的泛化性能呢?
- 原论文的解释是sign这个操作引入了额外的噪声(相比于准确的浮点值),它使得模型进入了Loss更平坦(但未必更小)的区域,从而泛化性能更好。为了验证这一点,作者比较了AdamW和Lion训练出来的模型权重的抗干扰能力,结果显示Lion的抗干扰能力更好。然而,理论上来说,这只能证明Lion确实进入到了更平坦的区域,但无法证明该结果是sign操作造成的。不过,Adam发表这么多年了,关于它的机理也还没有彻底研究清楚,而Lion只是刚刚提出,就不必过于吹毛求疵了。
- 笔者的猜测是,Lion通过sign操作平等地对待了每一个分量,使得模型充分地发挥了每一个分量的作用,从而有更好的泛化性能。如果SGD,那么更新的大小正比于它的梯度,然而有些分量梯度小,可能仅仅是因为它没初始化好,而并非它不重要,所以Lion的sign操作算是为每个参数都提供了“恢复活力”甚至“再创辉煌”的机会。事实上可以证明,Adam早期的更新量也接近于sign,只是随着训练步数的增加才逐渐偏离。
Lion是不是足够完美呢?
- 显然不是,比如原论文就指出它在小batch_size(小于64)的时候效果不如AdamW,这也不难理解,本来sign已经带来了噪声,而小batch_size则进一步增加了噪声,噪声这个东西,必须适量才好,所以两者叠加之下,很可能有噪声过量导致效果恶化。另外,也正因为sign加剧了优化过程的噪声,所以参数设置不当时容易出现损失变大等发散情况,这时候可以尝试引入Warmup,或者增加Warmup步数。还有,Lion依旧需要缓存动量参数,所以它的显存占用多于AdaFactor,能不能进一步优化这部分参数量呢?暂时还不得而知。
标准的Lion,在β1=β2时的特殊例子,这里称之为“Tiger”。
Tiger只用到了动量来构建更新量,根据《隐藏在动量中的梯度累积:少更新几步,效果反而更好?》的结论,此时我们不新增一组参数来“无感”地实现梯度累积!
这也意味着在我们有梯度累积需求时,Tiger已经达到了显存占用的最优解,这也是“Tiger”这个名字的来源(Tight-fisted Optimizer,抠门的优化器,不舍得多花一点显存)。
此外,Tiger还加入了我们的一些超参数调节经验,以及提出了一个防止模型出现NaN(尤其是混合精度训练下)的简单策略。我们的初步实验显示,Tiger的这些改动,能够更加友好地完成模型(尤其是大模型)的训练。
相比Lion,它就是选择了参数β1=β2=β;相比SignSGD,它则是新增了动量和权重衰减。
6.2.1 衰减率β
我们知道,在基本形式上Tiger相当于Lion取β1=β2=β的特殊情形,那么一个直觉是Tiger应当取β=12(β1+β2)。
在Lion的原论文中,对于CV任务有β1=0.9,β2=0.99,所以我们建议CV任务取β=0.945;
而对于NLP任务则有β1=0.95,β2=0.98,所以我们建议NLP任务取β=0.965。
6.2.2 学习率,
Tiger参考了Amos、LAMB等工作,将学习率分两种情况设置。
第一种是线性层的bias项和Normalization的beta、gamma参数,这类参数的特点是运算是element-wise,我们建议学习率选取为全局相对学习率αt的一半;
第二种主要就是线性层的kernel矩阵,这类参数的特点是以矩阵的身份去跟向量做矩阵乘法运算,我们建议学习率选取为全局相对学习率αt乘以参数本身的RMS(Root Mean Square)
这样设置的好处是我们把参数的尺度分离了出来,使得学习率的调控可以交给一个比较通用的“全局相对学习率”αt——大致可以理解为每一步的相对学习幅度,是一个对于模型尺度不是特别敏感的量。
换句话说,我们在base版模型上调好的αt,基本上可以不改动地用到large版模型。
注意αt带有下标t,所以它包含了整个学习率的schedule,包括Wamrup以及学习率衰减策略等,笔者的设置经验是max(αt)∈[0.001,0.002],至于怎么Warmup和衰减,那就是大家根据自己的任务而设了,别人无法代劳。笔者给的tiger实现,内置了一个分段线性学习率策略,理论上可以用它模拟任意的αt。
6.2.3 权重衰减率λt
这个Lion论文最后一页也给出了一些参考设置,一般来说λt也就设为常数,笔者常用的是0.01。
特别的是,不建议对前面说的bias、beta、gamma这三类参数做权重衰减,或者即便要做,λt也要低一个数量级以上。因为从先验分布角度来看,权重衰减是参数的高斯先验,λt跟参数方差是反比关系,而bias、beta、gamma的方差显然要比kernel矩阵的方差大,所以它们的λt应该更小。
6.2.4 梯度累积
对于很多算力有限的读者来说,通过梯度累积来增大batch_size是训练大模型时不可避免的一步。标准的梯度累积需要新增一组参数,用来缓存历史梯度,这意味着在梯度累积的需求下,Adam新增的参数是3组,Lion是2组,而即便是不加动量的AdaFactor也有1.x组(但说实话AdaFactor不加动量,收敛会慢很多,所以考虑速度的话,加一组动量就变为2.x组)。
而对于Tiger来说,它的更新量只用到了动量和原参数,根据《隐藏在动量中的梯度累积:少更新几步,效果反而更好?》,我们可以通过如下改动,将梯度累积内置在Tiger中:
可以看到,这仅仅相当于修改了滑动平均率β和学习率ηt,几乎不增加显存成本,整个过程是完全“无感”的,这是笔者认为的Tiger的最大的魅力。
需要指出的是,尽管Lion跟Tiger很相似,但是Lion并不能做到这一点,因为β1≠β2
时,Lion的更新需要用到动量以及当前批的梯度,这两个量需要用不同的参数缓存,而Tiger的更新只用到了动量,因此满足这一点。
类似滴,SGDM优化器也能做到一点,但是它没有sign操作,这意味着学习率的自适应能力不够好,在Transformer等模型上的效果通常不如意(参考《Why are Adaptive Methods Good for Attention Models?》)。
6.2.5 混合精度
混合精度,简单来说就是模型计算部分用半精度的FP16,模型参数的储存和更新部分用单精度的FP32。
之所以模型参数要用FP32,是因为担心更新过程中参数的更新量过小,下溢出了FP16的表示范围(大致是6×10?8~65504),导致某些参数长期不更新,模型训练进度慢甚至无法正常训练。
然而,Tiger(Lion也一样)对更新量做了sign运算,这使得理论上我们可以全用半精度训练!分析过程并不难。
首先,只要对Loss做适当的缩放,那么可以做到梯度gt不会溢出FP16的表示范围;
而动量mt只是梯度的滑动平均,梯度不溢出,它也不会溢出,
sign(mt)只能是±1,更加不会溢出了;
之后,我们只需要保证学习率不小于6×10?8,那么更新量就不会下溢了,事实上我们也不会将学习率调得这么小。
因此,Tiger的整个更新过程都是在FP16表示范围内的,因此理论上我们可以直接用全FP16精度训练而不用担心溢出问题。
然而,笔者发现对于同样的配置,在FP32下训练正常,但切换到混合精度或者半精度后有时会训练失败,具体表现后Loss先降后升然后NaN,
经过调试,笔者发现出现这种情况时,主要是对于某些batch梯度变为NaN,但此时模型的参数和前向计算还是正常的。
于是笔者就想了个简单的应对策略:对梯度出现NaN时,跳过这一步更新,并且对参数进行轻微收缩,如下:
其中s∈(0,1)代表收缩率,笔者取s=0.99,
c则是参数的初始化中心,一般就是gamma取1,
其他参数都是0。
经过这样处理后,模型的loss会有轻微上升,但一般能够恢复正常训练,不至于从头再来。
个人的实验结果显示,这样处理能够缓解一部分NaN的问题。
当然,该技巧一般的使用场景是同样配置下FP32能够正常训练,并且已经做好了epsilon、无穷大等混合精度调节,万般无奈之下才不得已使用的。如果模型本身超参数设置有问题(比如学习率过大),连FP32都会训练到NaN,那么就不要指望这个技巧能够解决问题了。此外,有兴趣的读者,还可以尝试改进这个技巧,比如收缩之后可以再加上一点噪声来增加参数的多样性,等等。
启发式方法指人在解决问题时所采取的一种根据经验规则进行发现的方法。其特点是在解决问题时,利用过去的经验,选择已经行之有效的方法,而不是系统地、以确定的步骤去寻求答案。启发式优化方法种类繁多,包括经典的模拟退火方法、遗传算法、蚁群算法以及粒子群算法等等。
它主要针对同时优化多个目标(两个及两个以上)的优化问题,这方面比较经典的算法有NSGAII算法、MOEA/D算法以及人工免疫算法等。这部分内容的介绍已经在博客《[Evolutionary Algorithm]进化算法简介》进行了概要式的介绍,有兴趣的博友可以进行参考(2015.12.13)。
拉格朗日乘子法主要用于解决约束优化问题,它的基本思想就是通过引入拉格朗日乘子来将含有n个变量和k个约束条件的约束优化问题转化为含有(n+k)个变量的无约束优化问题。拉格朗日乘子背后的数学意义是其为约束方程梯度线性组合中每个向量的系数。
通过引入拉格朗日乘子建立极值条件,对n个变量分别求偏导对应了n个方程,然后加上k个约束条件(对应k个拉格朗日乘子)一起构成包含了(n+k)变量的(n+k)个方程的方程组问题,这样就能根据求方程组的方法对其进行求解。